3.2. Mass Lumping for dual cell spaces

by M. Wess, 2024

This Notebook is part of the dualcellspaces documentation for the addon package implementing the Dual Cell method in NGSolve.

from ngsolve import *
import dualcellspaces as dcs
import matplotlib.pyplot as pl
import numpy as np

Dual cell integration rules

Since our spaces consist of functions which are smooth (polynomials) on the single cells (instead of the whole elements) we cannot use the standard integration rules provided by NGSolve for computing itegrals.

The dualcellspaces package provides dualcellspaces.GetIntegrationRules, which returns rules which respect the cell structure. These are not the integration nodes used for generating the spaces!

irs = dcs.GetIntegrationRules(2)
print(irs)

for et in irs:
  print(et)
  print(irs[et])

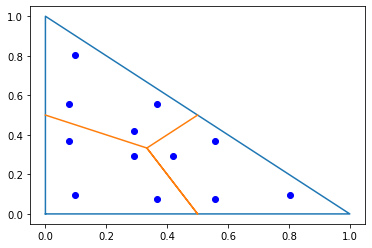
pl.plot([0,1,0,0],[0,0,1,0]);
pl.plot([0,1/3,0.5,1/3,0.5],[0.5,1/3,0,1/3,0.5]);

trig_points = np.array(irs[TRIG].points)
px,py = trig_points[:,0],trig_points[:,1]
pl.plot(px,py,'ob');

{<ET.SEGM: 1>: <ngsolve.fem.IntegrationRule object at 0x778e7007a3b0>, <ET.TRIG: 10>: <ngsolve.fem.IntegrationRule object at 0x778e7007a430>, <ET.TET: 20>: <ngsolve.fem.IntegrationRule object at 0x778e7007a4b0>}
ET.SEGM
 locnr = -1: (0.105662, 0, 0), weight = 0.25
 locnr = -1: (0.394338, 0, 0), weight = 0.25
 locnr = -1: (0.894338, 0, 0), weight = 0.25
 locnr = -1: (0.605662, 0, 0), weight = 0.25

ET.TRIG
 locnr = -1: (0.803561, 0.0982194, 0), weight = 0.0536948
 locnr = -1: (0.555556, 0.0778847, 0), weight = 0.0416667
 locnr = -1: (0.555556, 0.36656, 0), weight = 0.0416667
 locnr = -1: (0.418661, 0.290669, 0), weight = 0.0296385
 locnr = -1: (0.0982194, 0.803561, 0), weight = 0.0536948
 locnr = -1: (0.36656, 0.555556, 0), weight = 0.0416667
 locnr = -1: (0.0778847, 0.555556, 0), weight = 0.0416667
 locnr = -1: (0.290669, 0.418661, 0), weight = 0.0296385
 locnr = -1: (0.0982194, 0.0982194, 0), weight = 0.0536948
 locnr = -1: (0.0778847, 0.36656, 0), weight = 0.0416667
 locnr = -1: (0.36656, 0.0778847, 0), weight = 0.0416667
 locnr = -1: (0.290669, 0.290669, 0), weight = 0.0296385

ET.TET
 locnr = -1: (0.725312, 0.0915628, 0.0915628), weight = 0.00999851
 locnr = -1: (0.51153, 0.0733767, 0.0733767), weight = 0.00616387
 locnr = -1: (0.51153, 0.0733767, 0.341717), weight = 0.00616387
 locnr = -1: (0.391248, 0.0610607, 0.273846), weight = 0.00365801
 locnr = -1: (0.51153, 0.341717, 0.0733767), weight = 0.00616387
 locnr = -1: (0.391248, 0.273846, 0.0610607), weight = 0.00365801
 locnr = -1: (0.391248, 0.273846, 0.273846), weight = 0.00365801
 locnr = -1: (0.316355, 0.227882, 0.227882), weight = 0.0022025
 locnr = -1: (0.0915628, 0.725312, 0.0915628), weight = 0.00999851
 locnr = -1: (0.341717, 0.51153, 0.0733767), weight = 0.00616387
 locnr = -1: (0.0733767, 0.51153, 0.0733767), weight = 0.00616387
 locnr = -1: (0.273846, 0.391248, 0.0610607), weight = 0.00365801
 locnr = -1: (0.0733767, 0.51153, 0.341717), weight = 0.00616387
 locnr = -1: (0.273846, 0.391248, 0.273846), weight = 0.00365801
 locnr = -1: (0.0610607, 0.391248, 0.273846), weight = 0.00365801
 locnr = -1: (0.227882, 0.316355, 0.227882), weight = 0.0022025
 locnr = -1: (0.0915628, 0.0915628, 0.725312), weight = 0.00999851
 locnr = -1: (0.0733767, 0.341717, 0.51153), weight = 0.00616387
 locnr = -1: (0.341717, 0.0733767, 0.51153), weight = 0.00616387
 locnr = -1: (0.273846, 0.273846, 0.391248), weight = 0.00365801
 locnr = -1: (0.0733767, 0.0733767, 0.51153), weight = 0.00616387
 locnr = -1: (0.0610607, 0.273846, 0.391248), weight = 0.00365801
 locnr = -1: (0.273846, 0.0610607, 0.391248), weight = 0.00365801
 locnr = -1: (0.227882, 0.227882, 0.316355), weight = 0.0022025
 locnr = -1: (0.0915628, 0.0915628, 0.0915628), weight = 0.00999851
 locnr = -1: (0.0733767, 0.0733767, 0.341717), weight = 0.00616387
 locnr = -1: (0.0733767, 0.341717, 0.0733767), weight = 0.00616387
 locnr = -1: (0.0610607, 0.273846, 0.273846), weight = 0.00365801
 locnr = -1: (0.341717, 0.0733767, 0.0733767), weight = 0.00616387
 locnr = -1: (0.273846, 0.0610607, 0.273846), weight = 0.00365801
 locnr = -1: (0.273846, 0.273846, 0.0610607), weight = 0.00365801
 locnr = -1: (0.227882, 0.227882, 0.227882), weight = 0.0022025

Using these integration rules we may compute the exact mass matrices

order = 3

irs = dcs.GetIntegrationRules(2*order+2)
mesh = Mesh(unit_square.GenerateMesh(maxh=0.5))
fes = dcs.HCurlDualCells(mesh,order=order)
#fes = dcs.H1PrimalCells(mesh,order=order)
u,v = fes.TnT()

M = BilinearForm(u*v*dx(intrules=irs)).Assemble().mat
pl.spy(M.ToDense());

Mass lumping

We want to explot the fact that we used nodal basis functions with respect to the nodes of Gauss-Radau integration rules. Thus we need to assemble the mass matrices approximated by these integration rules.

irs_fes = fes.GetIntegrationRules()

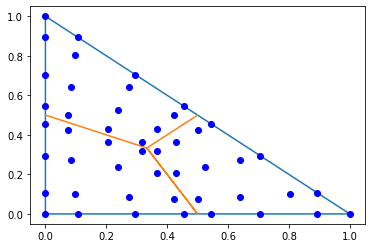
pl.plot([0,1,0,0],[0,0,1,0]);
pl.plot([0,1/3,0.5,1/3,0.5],[0.5,1/3,0,1/3,0.5]);

trig_points = np.array(irs_fes[TRIG].points)
px,py = trig_points[:,0],trig_points[:,1]
pl.plot(px,py,'ob');

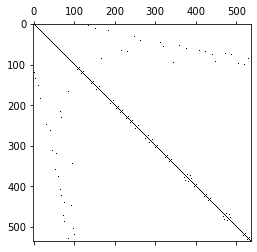
M = BilinearForm(u*v*dx(intrules=irs_fes)).Assemble().mat
pl.figure()
pl.spy(M.ToDense());
M_diag = M.DeleteZeroElements(1e-10)
pl.figure()
pl.spy(M_diag.ToDense());
#pl.spy(M.ToDense());

Exercises:

• Explain why we need apply the function DeleteZeroElements. Use the function BaseMatrix.nze to check the number of non-zero elements in the assembled matrix

• Look at the sparsity pattern of the exact and lumped mass matrix for the HCurlDualCells and H1DualCells spaces.

Application of (inverse) lumped mass matrices

Since the entries corresponding to basis functions of the dual elements are not stored together the block structure is less obvious here. Exploiting this block structure is implemented in the finite element spaces. The mass matrices may be accessed via FESpace.Mass:

from time import time

order = 3

irs = dcs.GetIntegrationRules(2*order+2)
mesh = Mesh(unit_cube.GenerateMesh(maxh=0.3))
fes = dcs.HCurlDualCells(mesh,order=order)

print("ndof = ",fes.ndof)

irs_fes = fes.GetIntegrationRules()
u,v = fes.TnT()

with TaskManager():
  now = time()
  M_exact = BilinearForm(u*v*dx(intrules=irs)).Assemble().mat
  exacttime = time()-now

  now = time()
  M_supersparse = fes.Mass()
  stime = time()-now

  print('#### assembling ####')
  print('exact: {}s'.format(exacttime))
  print('supersparse: {}s'.format(stime))


  now = time()
  M_exact_inv = M_exact.Inverse(inverse='sparsecholesky')
  exacttime = time()-now

  now = time()
  with TaskManager():
    M_supersparse_inv = M_supersparse.Inverse()
  stime = time()-now
  print('#### factorization ####')
  print('exact: {}s'.format(exacttime))
  print('supersparse: {}s'.format(stime))

  n = 10
  tmp = M_exact.CreateVector()
  tmp.SetRandom()
  tmp2 = M_exact.CreateVector()

  now = time()
  for i in range(n):
    tmp2.data = M_exact_inv * tmp
  exacttime = time()-now

  now = time()
  for i in range(n):
    tmp2.data = M_supersparse_inv * tmp
  stime = time()-now

  print('#### application ####')
  print('exact: {}s'.format(exacttime))
  print('supersparse: {}s'.format(stime))

ndof =  122352

#### assembling ####
exact: 1.8648200035095215s
supersparse: 0.16936349868774414s

#### factorization ####
exact: 21.143723249435425s
supersparse: 0.008497953414916992s

#### application ####
exact: 0.37490344047546387s
supersparse: 0.002124786376953125s