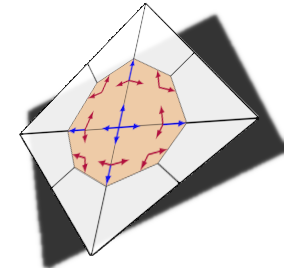
3.1. Basics on dual cell spaces

by M. Wess, 2024

This Notebook is part of the dualcellspaces documentation for the addon package implementing the Dual Cell method in NGSolve.

We start with doing the necessary imports

from ngsolve import *
import dualcellspaces as dcs
from ngsolve.webgui import Draw

The finite element spaces calles XXPrimalCells, XXDualCells, for the spaces on the primal and dual mesh respectively, where XX stands for H1, HCurl, HDiv.

The space H1PrimalCells

First we study the H1 space on the prmal mesh in two dimensions.

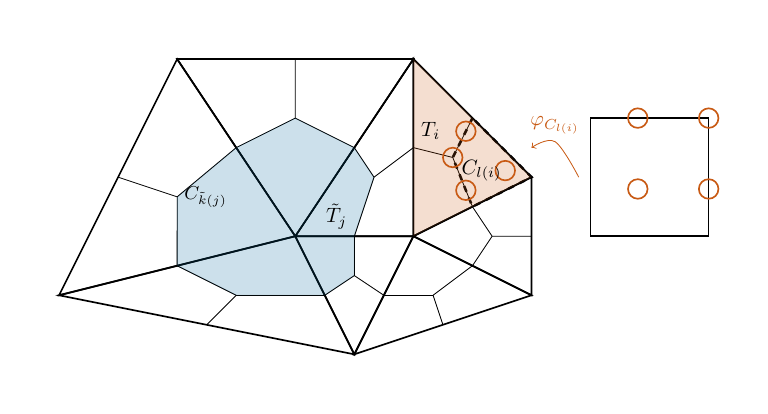
mesh = Mesh(unit_square.GenerateMesh())
Draw(mesh);
h1 = dcs.H1DualCells(mesh,order = 1)
print("number of elements in mesh: ", mesh.ne)
print("number of dofs per element: ", int(h1.ndof/mesh.ne))

number of elements in mesh:  2
number of dofs per element:  10

Let’s take a look at the basis functions:

gfu = GridFunction(h1,multidim = h1.ndof)
for i in range(h1.ndof):
    gfu.vecs[i][i] = 0.2
Draw(gfu, animate = True, min = 0, max = 0.2, intpoints = dcs.GetWebGuiPoints(2),order = 2, deformation = True, euler_angles =[-45,-6,25]);

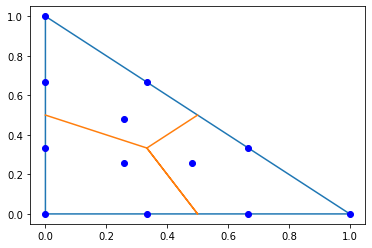
The basis functions are nodal basis functions with respect to a certain integration rule. We may extract the integration rule from the space:

import matplotlib.pyplot as pl
import numpy as np

irs_h1 = h1.GetIntegrationRules()

pl.plot([0,1,0,0],[0,0,1,0]);
pl.plot([0,1/3,0.5,1/3,0.5],[0.5,1/3,0,1/3,0.5]);

trig_points = np.array(irs_h1[TRIG].points)
px,py = trig_points[:,0],trig_points[:,1]
pl.plot(px,py,'ob');

Exercises

• Play around with orders: how many DoFs per element do you expect for the H1PrimalCells space depending on the polynomial order?

• Change the space to H1DualCells. How many global DoFs do you expect depending on the polynomial order?

The space HCurlDualCells

We study the HCurl space on the prmal mesh in two dimensions.

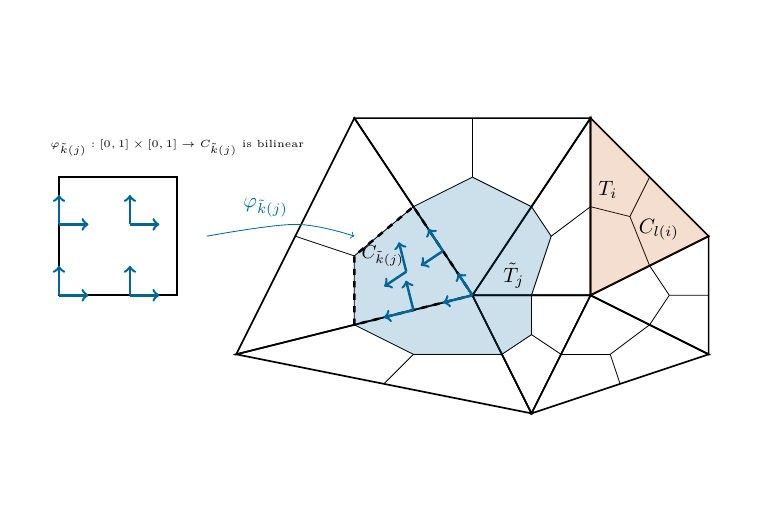
We create the space HCurlDualCells on a mesh with more elements to have inner vertices.

mesh_curl = Mesh(unit_square.GenerateMesh(maxh=0.435))
Draw(mesh_curl);
hcurl = dcs.HCurlDualCells(mesh_curl,order = 0)
print("number of (primal) elements in mesh: ", mesh_curl.ne)
print("number of dofs per element: ", hcurl.ndof/mesh_curl.ne)

number of (primal) elements in mesh:  14
number of dofs per element:  3.5714285714285716

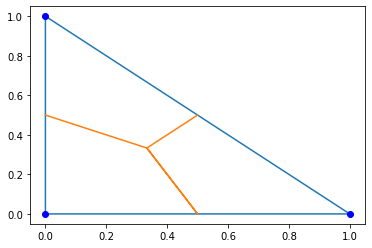
Again we may take a look at the corresponding integration rules:

irs_hcurl = hcurl.GetIntegrationRules()

pl.plot([0,1,0,0],[0,0,1,0]);
pl.plot([0,1/3,0.5,1/3,0.5],[0.5,1/3,0,1/3,0.5]);

trig_points = np.array(irs_hcurl[TRIG].points)
px,py = trig_points[:,0],trig_points[:,1]
pl.plot(px,py,'ob');
print(mesh_curl.nface, mesh_curl.ne)

14 14

Exercises

• Play around with orders: how many DoFs per vertex (Mesh.nv), edge (Mesh.nedge) and faces (in 2d equivalent: Mesh.ne, Mesh.nface)

3d spaces

In three dimensions the spaces are defined similarly. We construct the HCurl... spaces.

mesh = Mesh(unit_cube.GenerateMesh())
print("number of elements = {}".format(mesh.ne))
for order in range(5):
    print("###P = {}".format(order))
    print("ndof = {}".format(dcs.HCurlPrimalCells(mesh,order=order).ndof))
    print("{} * 4*(3*P^3+6*P^2+4*P+1)={}".format(mesh.ne,mesh.ne*4*(3*order**3+6*order**2+4*order+1)))

number of elements = 12
###P = 0
ndof = 48
12 * 4*(3*P^3+6*P^2+4*P+1)=48
###P = 1
ndof = 672
12 * 4*(3*P^3+6*P^2+4*P+1)=672
###P = 2
ndof = 2736
12 * 4*(3*P^3+6*P^2+4*P+1)=2736
###P = 3
ndof = 7104
12 * 4*(3*P^3+6*P^2+4*P+1)=7104
###P = 4
ndof = 14640
12 * 4*(3*P^3+6*P^2+4*P+1)=14640

print("number of elements = {}".format(mesh.ne))
for order in range(5):
    print("###P = {}".format(order))
    print("ndof = {}".format(dcs.HCurlDualCells(mesh,order=order).ndof))
    print("2*nedges*(P+1)+6*nfaces*P*(P+1)+12*nelements*P^2(P+1)={}".format(2*mesh.nedge*(order+1)+6*mesh.nface*(order+1)*order+12*mesh.ne*order**2*(order+1)))

number of elements = 12
###P = 0
ndof = 52
2*nedges*(P+1)+6*nfaces*P*(P+1)+12*nelements*P^2(P+1)=52
###P = 1
ndof = 752
2*nedges*(P+1)+6*nfaces*P*(P+1)+12*nelements*P^2(P+1)=752
###P = 2
ndof = 2964
2*nedges*(P+1)+6*nfaces*P*(P+1)+12*nelements*P^2(P+1)=2964
###P = 3
ndof = 7552
2*nedges*(P+1)+6*nfaces*P*(P+1)+12*nelements*P^2(P+1)=7552
###P = 4
ndof = 15380
2*nedges*(P+1)+6*nfaces*P*(P+1)+12*nelements*P^2(P+1)=15380