6. Calculating eigenvalues using PINVIT and LOBPCG#
Chirstoph Leonhartsberger
from ngsolve.la import InnerProduct, MultiVector
from ngsolve import Matrix, Vector
import scipy.linalg
from ngsolve import *
from netgen.csg import *
import numpy as np
def lobpcg(mata, matm, pre, num=1, maxit=20, printrates=True):
numIterations = 0
r = mata.CreateRowVector()
# using multivectors for better performance
uvecs = MultiVector(r, num)
vecs = MultiVector(r, 3 * num)
for v in vecs:
r.SetRandom()
v.data = pre * r
#uvecs[:] = pre * vecs[0:num]
lams = Vector(num * [1])
res = []
for i in range(maxit):
numIterations += 1
uvecs.data = mata * vecs[0:num] - (matm * vecs[0:num]).Scale(lams)
vecs[2*num:3*num] = pre * uvecs[0:num]
#T-norm res
resnorm=InnerProduct(uvecs[0],vecs[2*num])
for j in range(1, num):
tmp = InnerProduct(uvecs[j], vecs[2*num+j])
#print(tmp)
if (resnorm < tmp):
resnorm = tmp
res = np.append(res, resnorm)
vecs.Orthogonalize(matm)
asmall = InnerProduct(vecs, mata * vecs)
msmall = InnerProduct(vecs, matm * vecs)
ev, evec = scipy.linalg.eigh(a=asmall, b=msmall)
lams = Vector(ev[0:num])
if printrates:
print(i, ":", list(lams))
mat = Matrix(evec[:, 0:num])
uvecs[0:num] = vecs * mat
#print("res:", res[i], "\n")
if (res[i] < tol or i >= maxit):
print("iterationen:", i)
break
#use span{u^i,u^{i-1},w^i}
vecs[num:2*num] = vecs[0:num]
vecs[0:num] = uvecs[0:num]
return lams, uvecs, res
def PINVITres(mata, matm, pre, num=1, maxit=20, printrates=True):
"""preconditioned inverse iteration"""
r = mata.CreateRowVector()
uvecs = MultiVector(r, num)
vecs = MultiVector(r, 2*num)
# hv = MultiVector(r, 2*num)
for v in vecs:
r.SetRandom()
v.data = pre * r
lams = Vector(num * [1])
res = []
for i in range(maxit):
uvecs.data = mata * vecs[0:num] - (matm * vecs[0:num]).Scale (lams)
vecs[num:2*num] = pre * uvecs[0:num]
#T-norm res
resnorm=InnerProduct(uvecs[0],vecs[num])
for j in range(1, num):
tmp = InnerProduct(uvecs[j], vecs[num+j])
#print(tmp)
if (resnorm < tmp):
resnorm = tmp
res = np.append(res, resnorm)
vecs.Orthogonalize(matm)
asmall = InnerProduct (vecs, mata * vecs)
msmall = InnerProduct (vecs, matm * vecs)
ev,evec = scipy.linalg.eigh(a=asmall, b=msmall)
lams = Vector(ev[0:num])
if printrates:
print (i, ":", list(lams))
uvecs[:] = vecs * Matrix(evec[:,0:num])
vecs[0:num] = uvecs[0:num]
#print("res:", res[i], "\n")
if (res[i] < tol or i >= maxit):
print("iterationen:", i)
break
return lams, uvecs, res
6.1. Geometry used by Prof. J. Gerstmayr (EXUDYN)#
testgeom = 1
#1=conrod
#2=crank
#3=piston
#4=unit_cube
def geometry(type, meshSize):
if type == 1:
#parameters
#crank:
b1 = 0.012 #width of journal bearing
r1 = 0.012 #radius of journal bearing
dk = 0.015 #crank arm width (z)
bk = 0.032 #crank arm size (y)
l3 = 0.030
l4 = 0.040
#l4x= 0.005 #offset of counterweight
lk = 0.030 #l4*0.5+l3 #crank arm length (x)
bm = 0.065
dBevel = dk*0.5
#shaft:
r0 = 0.012 #0.012
d0 = 0.020 #shaft length at left/right support
d1 = 0.012 #shaft length at intermediate support
#distance rings:
db = 0.002 #width of distance ring
rdb0 = r0+db #total radius of distance ring, shaft
rdb1 = r1+db #total radius of distance ring, crank
#conrod:
bc = 0.024 #height of conrod
dc = 0.012 #width of conrod
lc = 0.080 #length of conrod (axis-axis)
r1o= r1+0.006 #outer radius of conrod at crank joint
r2 = 0.008 #radius of piston journal bearing
r2o= r2+0.006 #outer radius of conrod at piston joint
cylOffZ=0.010 #z-offset of cylinder cut out of conrod
cylR = 0.008 #radius of cylinder cut out of conrod
angC = 4*np.pi/180
#piston:
dpb = r2o-0.000 #axis inside piston
r2p = r2o+0.004 #0.018
lp = 0.034
bp = 0.050
lpAxis = dc+2*db
lOffCut = 0.011 #offset for cutout of big cylinder
#total length of one segment:
lTotal = db+dk+db+b1+db+dk+db+d1
#eps
eps = 5e-4 #added to faces, to avoid CSG-problems
def RotationMatrixZ(angleRad):
return np.array([ [np.cos(angleRad),-np.sin(angleRad), 0],
[np.sin(angleRad), np.cos(angleRad), 0],
[0, 0, 1] ]);
def VAdd(v0, v1):
if len(v0) != len(v1): print("ERROR in VAdd: incompatible vectors!")
n = len(v0)
v = [0]*n
for i in range(n):
v[i] = v0[i]+v1[i]
return v
def VSub(v0, v1):
if len(v0) != len(v1): print("ERROR in VSub: incompatible vectors!")
n = len(v0)
v = [0]*n
for i in range(n):
v[i] = v0[i]-v1[i]
return v
def NormL2(vector):
value = 0
for x in vector:
value += x**2
return value**0.5
def Normalize(v):
v2=[0]*len(v)
fact = NormL2(v)
fact = 1./fact
for i in range(len(v2)):
v2[i]=fact*v[i]
return v2
def GenerateConrod(zOff):
ey0 = [0,1,0] #top/bottom face vector of conrod
ey1 = [0,-1,0]
ex0 = [1,0,0] #top/bottom face vector of conrod
ex1 = [1,0,0]
ey0 = RotationMatrixZ(-angC)@ey0
ey1 = RotationMatrixZ(angC)@ey1
ex0 = RotationMatrixZ(-angC)@ex0
ex1 = RotationMatrixZ(angC)@ex1
pl1 = Plane(Pnt(0, 0.5*bc,0),Vec(ey0[0],ey0[1],ey0[2]))
pl2 = Plane(Pnt(0,-0.5*bc,0),Vec(ey1[0],ey1[1],ey1[2]))
pl3 = Plane(Pnt(-0.5*lc,0,0),Vec(-1,0,0))
pl4 = Plane(Pnt( 0.5*lc,0,0),Vec( 1,0,0))
pl5 = Plane(Pnt( 0,0,-0.5*dc+zOff),Vec( 0,0,-1))
pl6 = Plane(Pnt( 0,0, 0.5*dc+zOff),Vec( 0,0, 1))
cylC1 = Cylinder(Pnt(-0.5*lc,0,-1), Pnt(-0.5*lc,0,1), r1)
#cylC1o = Cylinder(Pnt(-0.5*lc,0,-1), Pnt(-0.5*lc,0,1), r1o)
cylC1o = Sphere(Pnt(-0.5*lc,0,zOff), r1o) #in fact is a sphere
cylC2 = Cylinder(Pnt( 0.5*lc,0,-1), Pnt( 0.5*lc,0,1), r2)
#cylC2o = Cylinder(Pnt(0.5*lc,0,-1), Pnt( 0.5*lc,0,1), r2o)
cylC2o = Sphere(Pnt(0.5*lc,0,zOff), r2o) #in fact is a sphere
cylSideA = (Cylinder(Pnt(-0.5*lc+r1o,0,cylOffZ+zOff), Pnt(0.5*lc-r2o,0,cylOffZ+zOff), cylR)*
Plane(Pnt(-0.5*lc+r1o-0.002,0,0),Vec(-1,0,0))*
Plane(Pnt( 0.5*lc-r2o+0.002,0,0),Vec( 1,0,0)))
cylSideB = (Cylinder(Pnt(-0.5*lc+r1o,0,-cylOffZ+zOff), Pnt(0.5*lc-r2o,0,-cylOffZ+zOff), cylR)*
Plane(Pnt(-0.5*lc+r1o-0.002,0,0),Vec(-1,0,0))*
Plane(Pnt( 0.5*lc-r2o+0.002,0,0),Vec( 1,0,0)))
return ((pl1*pl2*pl3*pl4+cylC1o+cylC2o)-cylC1-cylC2)*pl5*pl6-cylSideA-cylSideB
#return pl1*pl2*pl3*pl4*pl5*pl6
geoConrod = CSGeometry()
conrod = GenerateConrod(0)#db+dk+db+0.5*b1
geoConrod.Add(conrod)
mesh = Mesh(geoConrod.GenerateMesh(maxh=meshSize+0.001*0))
if type == 2:
#crank:
b1 = 0.012 #width of journal bearing
r1 = 0.012 #radius of journal bearing
dk = 0.015 #crank arm width (z)
bk = 0.032 #crank arm size (y)
l3 = 0.030
l4 = 0.040
#l4x= 0.005 #offset of counterweight
lk = 0.030 #l4*0.5+l3 #crank arm length (x)
bm = 0.065
dBevel = dk*0.5
#shaft:
r0 = 0.012 #0.012
d0 = 0.020 #shaft length at left/right support
d1 = 0.012 #shaft length at intermediate support
#distance rings:
db = 0.002 #width of distance ring
rdb0 = r0+db #total radius of distance ring, shaft
rdb1 = r1+db #total radius of distance ring, crank
#conrod:
bc = 0.024 #height of conrod
dc = 0.012 #width of conrod
lc = 0.080 #length of conrod (axis-axis)
r1o= r1+0.006 #outer radius of conrod at crank joint
r2 = 0.008 #radius of piston journal bearing
r2o= r2+0.006 #outer radius of conrod at piston joint
cylOffZ=0.010 #z-offset of cylinder cut out of conrod
cylR = 0.008 #radius of cylinder cut out of conrod
angC = 4*np.pi/180
#piston:
dpb = r2o-0.000 #axis inside piston
r2p = r2o+0.004 #0.018
lp = 0.034
bp = 0.050
lpAxis = dc+2*db
lOffCut = 0.011 #offset for cutout of big cylinder
#total length of one segment:
lTotal = db+dk+db+b1+db+dk+db+d1
#eps
eps = 5e-4 #added to faces, to avoid CSG-problems
def RotationMatrixZ(angleRad):
return np.array([ [np.cos(angleRad),-np.sin(angleRad), 0],
[np.sin(angleRad), np.cos(angleRad), 0],
[0, 0, 1] ]);
def VAdd(v0, v1):
if len(v0) != len(v1): print("ERROR in VAdd: incompatible vectors!")
n = len(v0)
v = [0]*n
for i in range(n):
v[i] = v0[i]+v1[i]
return v
def VSub(v0, v1):
if len(v0) != len(v1): print("ERROR in VSub: incompatible vectors!")
n = len(v0)
v = [0]*n
for i in range(n):
v[i] = v0[i]-v1[i]
return v
def NormL2(vector):
value = 0
for x in vector:
value += x**2
return value**0.5
def Normalize(v):
v2=[0]*len(v)
fact = NormL2(v)
fact = 1./fact
for i in range(len(v2)):
v2[i]=fact*v[i]
return v2
#points
pLB = [0 ,0,-d0]
p0B = [0 ,0,0]
p1B = [0 ,0,db]
#p2B = [0, 0,db+dk]
p21B =[lk,0,db+dk]
p31B = [lk,0,db+dk+db]
p41B = [lk,0,db+dk+db+b1]
p51B =[lk,0,db+dk+db+b1+db]
p6B = [0 ,0,db+dk+db+b1+db+dk]
p7B = [0 ,0,db+dk+db+b1+db+dk+db]
p8B = [0 ,0,lTotal]
def CSGcylinder(p0,p1,r):
v = VSub(p1,p0)
v = Normalize(v)
cyl = Cylinder(Pnt(p0[0],p0[1],p0[2]), Pnt(p1[0],p1[1],p1[2]),
r) * Plane(Pnt(p0[0],p0[1],p0[2]), Vec(-v[0],-v[1],-v[2])) * Plane(Pnt(p1[0],p1[1],p1[2]), Vec(v[0],v[1],v[2]))
return cyl
def CSGcube(pCenter,size):
s2 = [0.5*size[0],0.5*size[1],0.5*size[2]]
p0 = VSub(pCenter,s2)
p1 = VAdd(pCenter,s2)
brick = OrthoBrick(Pnt(p0[0],p0[1],p0[2]),Pnt(p1[0],p1[1],p1[2]))
return brick
#transform points
def TransformCrank(p, zOff, zRot):
p2 = RotationMatrixZ(zRot) @ p
pOff=[0,0,zOff]
return VAdd(p2,pOff)
#cube only in XY-plane, z infinite
def CSGcubeXY(pCenter,sizeX,sizeY,ex,ey):
#print("pCenter=",pCenter)
pl1 = Plane(Pnt(pCenter[0]-0.5*sizeX*ex[0],pCenter[1]-0.5*sizeX*ex[1],0),Vec(-ex[0],-ex[1],-ex[2]))
pl2 = Plane(Pnt(pCenter[0]+0.5*sizeX*ex[0],pCenter[1]+0.5*sizeX*ex[1],0),Vec( ex[0], ex[1], ex[2]))
pl3 = Plane(Pnt(pCenter[0]-0.5*sizeY*ey[0],pCenter[1]-0.5*sizeY*ey[1],0),Vec(-ey[0],-ey[1],-ey[2]))
pl4 = Plane(Pnt(pCenter[0]+0.5*sizeY*ey[0],pCenter[1]+0.5*sizeY*ey[1],0),Vec( ey[0], ey[1], ey[2]))
return pl1*pl2*pl3*pl4
#create one crank face at certain z-offset and rotation; side=1: left, side=-1: right
def GetCrankFace(zOff, zRot, side=1):
ex = RotationMatrixZ(zRot) @ [1,0,0]
ey = RotationMatrixZ(zRot) @ [0,1,0]
#print("zOff=",zOff, "zRot=", zRot, "side=", side,"ex=", ex)
pLeft = [0,0,zOff]
pRight = [0,0,zOff+dk]
pMid = [0,0,zOff+0.5*dk]
pcLeft=VAdd(pLeft,lk*ex)
pcRight=VAdd(pRight,lk*ex)
f=0.5**0.5
cyl1pl = Plane(Pnt(pcLeft[0],pcLeft[1],pcLeft[2]+0.5*dk-side*dk),Vec(f*ex[0],f*ex[1],f*ex[2]-side*f))
cyl1 = Cylinder(Pnt(pcLeft[0],pcLeft[1],pcLeft[2]-1), Pnt(pcRight[0],pcRight[1],pcRight[2]+1), 0.5*bk)*cyl1pl
#cone2 = Cylinder(Pnt(pcLeft[0],pcLeft[1],pcLeft[2]-1), Pnt(pcRight[0],pcRight[1],pcRight[2]+1), lk+l4)
cone2 = Cone(Pnt(pcLeft[0],pcLeft[1],pcLeft[2]-side*dBevel+0.5*dk), Pnt(pcLeft[0],pcLeft[1],pcLeft[2]+side*dBevel+0.5*dk), lk+l4-1.5*dBevel, lk+l4-0.5*dBevel)
cube1 = CSGcubeXY(VAdd(pMid,0.49*l3*ex),1.02*l3,bk,ex,ey) #make l3 a little longer, to avoid bad edges
cube2 = CSGcubeXY(VAdd(pMid,-0.5*l4*ex),1.0*l4,bm,ex,ey)*cone2
pc3a = VAdd(pLeft,0.*l3*ex+(0.5*bk+0.4*l3)*ey)
cyl3a = Cylinder(Pnt(pc3a[0],pc3a[1],pc3a[2]-1), Pnt(pc3a[0],pc3a[1],pc3a[2]+1), 0.42*l3)
pc3b = VAdd(pLeft,0.*l3*ex+(-0.5*bk-0.4*l3)*ey)
cyl3b = Cylinder(Pnt(pc3b[0],pc3b[1],pc3b[2]-1), Pnt(pc3b[0],pc3b[1],pc3b[2]+1), 0.42*l3)
#cube3a = (CSGcubeXY(VAdd(pMid,0.26*l3*ex+(0.5*bk+0.26*l3)*ey),0.5*l3,0.5*l3,ex,ey)-cyl3a)
return ((cube1+cube2+cyl1)-(cyl3a+cyl3b))*Plane(Pnt(0,0,pLeft[2]),Vec(0,0,-1))*Plane(Pnt(0,0,pRight[2]),Vec(0,0,1))
#return (cube1+cube2+cyl1)*Plane(Pnt(0,0,pLeft[2]),Vec(0,0,-1))*Plane(Pnt(0,0,pRight[2]),Vec(0,0,1))
#generate one crank, rotated around z-axis in radiant
def GenerateCrank(zOff, zRot):
pL = TransformCrank(pLB,zOff, zRot)
p0 = TransformCrank(p0B,zOff, zRot)
p1 = TransformCrank(p1B,zOff, zRot)
p21 = TransformCrank(p21B,zOff, zRot)
p31 = TransformCrank(p31B,zOff, zRot)
p41 = TransformCrank(p41B,zOff, zRot)
p51 = TransformCrank(p51B,zOff, zRot)
p6 = TransformCrank(p6B,zOff, zRot)
p7 = TransformCrank(p7B,zOff, zRot)
p8 = TransformCrank(p8B,zOff, zRot)
crank0 = CSGcylinder(pL,[p0[0],p0[1],p0[2]+eps],r0)
crank1 = CSGcylinder(p0,[p1[0],p1[1],p1[2]+eps],rdb0)
#conrod bearing:
crank3 = CSGcylinder([p21[0],p21[1],p21[2]-eps],p31,rdb1)
crank7 = CSGcylinder(p31,p41,r1)
crank8 = CSGcylinder(p41,[p51[0],p51[1],p51[2]+eps],rdb1)
crank9 = CSGcylinder([p6[0],p6[1],p6[2]-eps],p7,rdb0)
crank10 = CSGcylinder([p7[0],p7[1],p7[2]-eps],p8,r0)
#return crank0+crank1+crank3+crank4+crank5+crank6+crank7+crank8+crank4b+crank5b+crank6b+crank9+crank10
if zOff==0:#add first shaft
crank1 = crank1+crank0
return crank1+GetCrankFace(db+zOff,zRot,1)+crank3+crank7+crank8+GetCrankFace(db+2*db+dk+b1+zOff,zRot,-1)+crank10+crank9
#++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
#choose configuration for crankshaft:
#crankConfig = [0] #1-piston
#crankConfig = [np.pi/2] #1-piston
#crankConfig = [0,np.pi] #2-piston
#crankConfig = [0,np.pi*2./3.,2.*np.pi*2./3.] #3-piston
#crankConfig = [0,np.pi,np.pi,0] #4-piston
crankConfig = [0,np.pi*2./3.,2.*np.pi*2./3.,2.*np.pi*2./3.,np.pi*2./3.,0] #6-piston
nPistons = len(crankConfig)
crank = GenerateCrank(0, crankConfig[0])
zPos = lTotal
for i in range(len(crankConfig)-1):
angle = crankConfig[i+1]
crank += GenerateCrank(zPos, angle)
zPos += lTotal
# crank = (GenerateCrank(0, 0) + GenerateCrank(lTotal, np.pi*2./3.) + GenerateCrank(2*lTotal, np.pi*2.*2./3.)+
# GenerateCrank(3*lTotal, np.pi*2.*2./3.) + GenerateCrank(4*lTotal, np.pi*2./3.))
geoCrank = CSGeometry()
geoCrank.Add(crank)
mesh = Mesh( geoCrank.GenerateMesh(maxh=meshSize+0.001*0))
if type == 3:
#crank:
b1 = 0.012 #width of journal bearing
r1 = 0.012 #radius of journal bearing
dk = 0.015 #crank arm width (z)
bk = 0.032 #crank arm size (y)
l3 = 0.030
l4 = 0.040
#l4x= 0.005 #offset of counterweight
lk = 0.030 #l4*0.5+l3 #crank arm length (x)
bm = 0.065
dBevel = dk*0.5
#shaft:
r0 = 0.012 #0.012
d0 = 0.020 #shaft length at left/right support
d1 = 0.012 #shaft length at intermediate support
#distance rings:
db = 0.002 #width of distance ring
rdb0 = r0+db #total radius of distance ring, shaft
rdb1 = r1+db #total radius of distance ring, crank
#conrod:
bc = 0.024 #height of conrod
dc = 0.012 #width of conrod
lc = 0.080 #length of conrod (axis-axis)
r1o= r1+0.006 #outer radius of conrod at crank joint
r2 = 0.008 #radius of piston journal bearing
r2o= r2+0.006 #outer radius of conrod at piston joint
cylOffZ=0.010 #z-offset of cylinder cut out of conrod
cylR = 0.008 #radius of cylinder cut out of conrod
angC = 4*np.pi/180
#piston:
dpb = r2o-0.000 #axis inside piston
r2p = r2o+0.004 #0.018
lp = 0.034
bp = 0.050
lpAxis = dc+2*db
lOffCut = 0.011 #offset for cutout of big cylinder
#total length of one segment:
lTotal = db+dk+db+b1+db+dk+db+d1
#eps
eps = 5e-4 #added to faces, to avoid CSG-problems
def NormL2(vector):
value = 0
for x in vector:
value += x**2
return value**0.5
def Normalize(v):
v2=[0]*len(v)
fact = NormL2(v)
fact = 1./fact
for i in range(len(v2)):
v2[i]=fact*v[i]
return v2
def VAdd(v0, v1):
if len(v0) != len(v1): print("ERROR in VAdd: incompatible vectors!")
n = len(v0)
v = [0]*n
for i in range(n):
v[i] = v0[i]+v1[i]
return v
def VSub(v0, v1):
if len(v0) != len(v1): print("ERROR in VSub: incompatible vectors!")
n = len(v0)
v = [0]*n
for i in range(n):
v[i] = v0[i]-v1[i]
return v
def CSGcube(pCenter,size):
s2 = [0.5*size[0],0.5*size[1],0.5*size[2]]
p0 = VSub(pCenter,s2)
p1 = VAdd(pCenter,s2)
brick = OrthoBrick(Pnt(p0[0],p0[1],p0[2]),Pnt(p1[0],p1[1],p1[2]))
return brick
def CSGcylinder(p0,p1,r):
v = VSub(p1,p0)
v = Normalize(v)
cyl = Cylinder(Pnt(p0[0],p0[1],p0[2]), Pnt(p1[0],p1[1],p1[2]),
r) * Plane(Pnt(p0[0],p0[1],p0[2]), Vec(-v[0],-v[1],-v[2])) * Plane(Pnt(p1[0],p1[1],p1[2]), Vec(v[0],v[1],v[2]))
return cyl
def GeneratePiston(zOff):
p0 = [-dpb,0,zOff]
p1 = [-dpb+lp,0,zOff]
cylPo = CSGcylinder(p0, p1, 0.5*bp) #piston outside
cylPaxis= CSGcylinder([0,0,-0.5*lpAxis-eps+zOff], [0,0, 0.5*lpAxis+eps+zOff], r2) #piston axis
cylPaxis0= CSGcylinder([0,0,-0.5*lpAxis-eps+zOff], [0,0,-0.5*lpAxis+db+zOff], r2+db) #piston axis
cylPaxis1= CSGcylinder([0,0, 0.5*lpAxis-db+zOff], [0,0, 0.5*lpAxis+eps+zOff], r2+db) #piston axis
cylPin = CSGcylinder([0,0,-0.5*lpAxis+zOff], [0,0, 0.5*lpAxis+zOff], r2p) #piston inner cutout
#box = CSGcube([0,0,zOff], [dpb+r2p,2*(r2p),lpAxis])
box = CSGcube([-0.5*dpb,0,zOff], [dpb,2*(r2p)-0.002,lpAxis-0.000])
cylCut = CSGcylinder([-(l4+l3+lOffCut),0,-bp+zOff], [-(l4+l3+lOffCut),0, bp+zOff], l4+l3) #piston inner cutout
return (cylPo-box-cylCut-cylPin)+cylPaxis+cylPaxis0+cylPaxis1
geoPiston = CSGeometry()
piston = GeneratePiston(0)#db+dk+db+0.5*b1
geoPiston.Add(piston)
mesh = Mesh(geoPiston.GenerateMesh(maxh=meshSize+0.001*0))
if type == 4:
cube = OrthoBrick( Pnt(0,0,0), Pnt(1,1,1) )
geo = CSGeometry()
geo.Add (cube)
ngmesh = geo.GenerateMesh(maxh=0.075)
mesh = Mesh(ngmesh)
return mesh
mesh = geometry(1, 0.002)
from ngsolve.webgui import Draw
Draw(mesh)
print(mesh.ne)
12475
6.2. Linear elasticity setup#
meshOrder = 2
elOrder = 2
if meshOrder == 2:
mesh.ngmesh.SecondOrder()
fes = VectorH1(mesh, order=elOrder)
u = fes.TrialFunction()
v = fes.TestFunction()
bfK = BilinearForm(fes)
bfM = BilinearForm(fes)
def sigma(eps, mu, lam):
return 2*mu*eps + lam*Trace(eps) * Id(eps.dims[0])
density = 7850
youngsModulus = 2.1e11 *1e-1
poissonsRatio = 0.3
E = youngsModulus
nu = poissonsRatio
rho = density
mu = E / 2 / (1+nu)
lam = E * nu / ((1+nu)*(1-2*nu))
bfK += InnerProduct(sigma(Sym(Grad(u)),mu,lam), Sym(Grad(v)))*dx
bfM += rho*u*v * dx
bfK.Assemble()
bfM.Assemble()
<ngsolve.comp.BilinearForm at 0x11f147770>
6.3. BDDC preconditioner with vertices in wirebasket#
ndscal = fes.ndof // mesh.dim
nv = mesh.nv
fes.SetCouplingType(IntRange(0, fes.ndof), COUPLING_TYPE.INTERFACE_DOF)
fes.SetCouplingType(IntRange(0, nv), COUPLING_TYPE.WIREBASKET_DOF)
fes.SetCouplingType(IntRange(ndscal, ndscal + nv), COUPLING_TYPE.WIREBASKET_DOF)
fes.SetCouplingType(IntRange(2*ndscal, 2*ndscal + nv), COUPLING_TYPE.WIREBASKET_DOF)
F = specialcf.JacobianMatrix(3)
cond = Norm(F) * Norm(Inv(F))
ir = IntegrationRule([(1/4,1/4,1/4)], [1])
for el in mesh.Elements(VOL):
trafo = mesh.GetTrafo(el)
mir = trafo(ir)
condT = max(cond(mir))
if condT > 8:
for i in fes.GetDofNrs(el):
fes.SetCouplingType(i, COUPLING_TYPE.WIREBASKET_DOF)
#print (condT)
with TaskManager():
bfKbddc = BilinearForm(fes, eliminate_internal=True)
bfKbddc += InnerProduct(sigma(Sym(Grad(u)), mu, lam), Sym(Grad(v))) *dx
bfKbddc += 1e6*rho*u*v *dx
prebddc = Preconditioner(bfKbddc, "bddc")
bfKbddc.Assemble()
tol = 1e-10
it = 500
lams, evecs, reslop = lobpcg(bfK.mat, bfM.mat, prebddc, num=1, maxit=it, printrates=False)
iterationen: 90
lams,evecs, respinv = PINVITres(bfK.mat, bfM.mat, prebddc, num=1, maxit=it, printrates=False)
import numpy as np
import matplotlib.pyplot as plt
# Generate x-axis values based on array length
x = np.arange(1,len(respinv)+1)
# Plotting the array
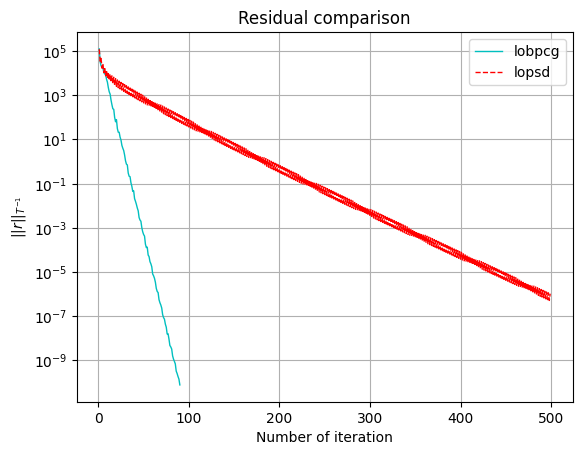
plt.semilogy(list(range(1,len(reslop))),reslop[1:len(reslop)],color="c",linestyle="-",linewidth=1,label="lobpcg")
plt.semilogy(list(range(1,len(respinv))),respinv[1:len(respinv)],color="r",linestyle="--",linewidth=1,label="lopsd")
plt.xlabel('Number of iteration')
plt.ylabel(r'$||r||_{T^{-1}}$')
plt.title('Residual comparison')
plt.grid(True)
plt.legend()
plt.show()
6.4. Time comparison#
import time
meshsizes = [0.01 - i * (0.01 - 0.002) / 7 for i in range(8)]
times_lobpcg = []
times_pinvit = []
for input_val in meshsizes:
mesh = geometry(1, input_val)
print(mesh.ne)
meshOrder = 2
elOrder = 2
if meshOrder == 2:
mesh.ngmesh.SecondOrder()
fes = VectorH1(mesh, order=elOrder)
u = fes.TrialFunction()
v = fes.TestFunction()
bfK = BilinearForm(fes)
bfM = BilinearForm(fes)
def sigma(eps, mu, lam):
return 2*mu*eps + lam*Trace(eps) * Id(eps.dims[0])
density = 7850
youngsModulus = 2.1e11 *1e-1
poissonsRatio = 0.3
E = youngsModulus
nu = poissonsRatio
rho = density
mu = E / 2 / (1+nu)
lam = E * nu / ((1+nu)*(1-2*nu))
bfK += InnerProduct(sigma(Sym(Grad(u)),mu,lam), Sym(Grad(v)))*dx
bfM += rho*u*v * dx
bfK.Assemble()
bfM.Assemble()
ndscal = fes.ndof // mesh.dim
nv = mesh.nv
fes.SetCouplingType(IntRange(0, fes.ndof), COUPLING_TYPE.INTERFACE_DOF)
fes.SetCouplingType(IntRange(0, nv), COUPLING_TYPE.WIREBASKET_DOF)
fes.SetCouplingType(IntRange(ndscal, ndscal + nv), COUPLING_TYPE.WIREBASKET_DOF)
fes.SetCouplingType(IntRange(2*ndscal, 2*ndscal + nv), COUPLING_TYPE.WIREBASKET_DOF)
F = specialcf.JacobianMatrix(3)
cond = Norm(F) * Norm(Inv(F))
ir = IntegrationRule([(1/4,1/4,1/4)], [1])
for el in mesh.Elements(VOL):
trafo = mesh.GetTrafo(el)
mir = trafo(ir)
condT = max(cond(mir))
if condT > 8:
for i in fes.GetDofNrs(el):
fes.SetCouplingType(i, COUPLING_TYPE.WIREBASKET_DOF)
#print (condT)
with TaskManager():
bfKbddc = BilinearForm(fes, eliminate_internal=True)
bfKbddc += InnerProduct(sigma(Sym(Grad(u)), mu, lam), Sym(Grad(v))) *dx
bfKbddc += 1e6*rho*u*v *dx
prebddc = Preconditioner(bfKbddc, "bddc")
bfKbddc.Assemble()
tol = 1e-5
it = 500
start_time = time.time()
lams, evecs, reslop = lobpcg(bfK.mat, bfM.mat, prebddc, num=1, maxit=it, printrates=False)
end_time = time.time()
times_lobpcg.append(end_time - start_time)
start_time = time.time()
lams,evecs, respinv = PINVITres(bfK.mat, bfM.mat, prebddc, num=1, maxit=it, printrates=False)
end_time = time.time()
times_pinvit.append(end_time - start_time)
930
iterationen: 47
iterationen: 287
928
iterationen: 47
iterationen: 283
940
iterationen: 46
iterationen: 289
952
iterationen: 49
iterationen: 327
1067
iterationen: 59
iterationen: 496
1437
iterationen: 52
iterationen: 350
2734
iterationen: 67
12475
iterationen: 60
iterationen: 440
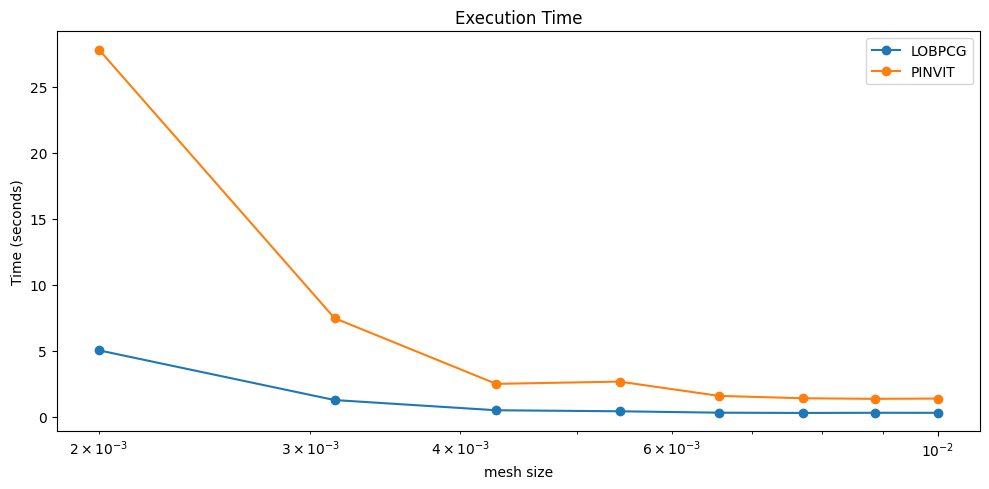
6.5. Time comparison for fixed tolerance and changing DOFs (tau = 1e-5)#
plt.figure(figsize=(10, 5))
plt.semilogx(meshsizes, times_lobpcg, label='LOBPCG', marker='o')
plt.semilogx(meshsizes, times_pinvit, label='PINVIT', marker='o')
plt.xlabel('mesh size')
plt.ylabel('Time (seconds)')
plt.title('Execution Time')
plt.legend()
plt.tight_layout()
plt.show()
tolerances = [1e-2 * (1e-1)**i for i in range(8)]
import time
times_lobpcg = []
times_pinvit = []
mesh = geometry(3, 0.01)
for tau in tolerances:
meshOrder = 2
elOrder = 2
if meshOrder == 2:
mesh.ngmesh.SecondOrder()
fes = VectorH1(mesh, order=elOrder)
u = fes.TrialFunction()
v = fes.TestFunction()
bfK = BilinearForm(fes)
bfM = BilinearForm(fes)
def sigma(eps, mu, lam):
return 2*mu*eps + lam*Trace(eps) * Id(eps.dims[0])
density = 7850
youngsModulus = 2.1e11 *1e-1
poissonsRatio = 0.3
E = youngsModulus
nu = poissonsRatio
rho = density
mu = E / 2 / (1+nu)
lam = E * nu / ((1+nu)*(1-2*nu))
bfK += InnerProduct(sigma(Sym(Grad(u)),mu,lam), Sym(Grad(v)))*dx
bfM += rho*u*v * dx
bfK.Assemble()
bfM.Assemble()
ndscal = fes.ndof // mesh.dim
nv = mesh.nv
fes.SetCouplingType(IntRange(0, fes.ndof), COUPLING_TYPE.INTERFACE_DOF)
fes.SetCouplingType(IntRange(0, nv), COUPLING_TYPE.WIREBASKET_DOF)
fes.SetCouplingType(IntRange(ndscal, ndscal + nv), COUPLING_TYPE.WIREBASKET_DOF)
fes.SetCouplingType(IntRange(2*ndscal, 2*ndscal + nv), COUPLING_TYPE.WIREBASKET_DOF)
F = specialcf.JacobianMatrix(3)
cond = Norm(F) * Norm(Inv(F))
ir = IntegrationRule([(1/4,1/4,1/4)], [1])
for el in mesh.Elements(VOL):
trafo = mesh.GetTrafo(el)
mir = trafo(ir)
condT = max(cond(mir))
if condT > 8:
for i in fes.GetDofNrs(el):
fes.SetCouplingType(i, COUPLING_TYPE.WIREBASKET_DOF)
#print (condT)
with TaskManager():
bfKbddc = BilinearForm(fes, eliminate_internal=True)
bfKbddc += InnerProduct(sigma(Sym(Grad(u)), mu, lam), Sym(Grad(v))) *dx
bfKbddc += 1e6*rho*u*v *dx
prebddc = Preconditioner(bfKbddc, "bddc")
bfKbddc.Assemble()
tol = tau
it = 700
start_time = time.time()
lams, evecs, reslop = lobpcg(bfK.mat, bfM.mat, prebddc, num=1, maxit=it, printrates=False)
end_time = time.time()
times_lobpcg.append(end_time - start_time)
start_time = time.time()
lams,evecs, respinv = PINVITres(bfK.mat, bfM.mat, prebddc, num=1, maxit=it, printrates=False)
end_time = time.time()
times_pinvit.append(end_time - start_time)
iterationen: 44
iterationen: 303
iterationen: 48
iterationen: 351
iterationen: 53
iterationen: 404
iterationen: 58
iterationen: 452
iterationen: 62
iterationen: 503
iterationen: 68
iterationen: 548
iterationen: 74
iterationen: 596
iterationen: 77
iterationen: 642
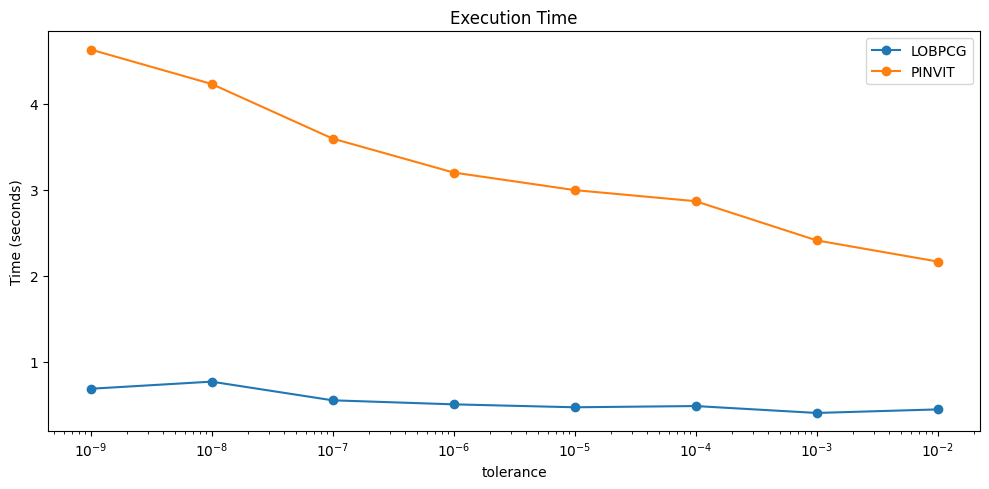
6.6. Time comparison for fixed DOFs and changing tolerance#
plt.figure(figsize=(10, 5))
plt.semilogx(tolerances, times_lobpcg, label='LOBPCG', marker='o')
plt.semilogx(tolerances, times_pinvit, label='PINVIT', marker='o')
plt.xlabel('tolerance')
plt.ylabel('Time (seconds)')
plt.title('Execution Time')
plt.legend()
plt.tight_layout()
plt.show()